執筆者：Andrea Allievi
、Holger Unterbrink
概要
ランサムウェアとは、ユーザのファイル（写真、ドキュメント、音楽など）を身代金目的で暗号化し、その復号のために金銭を要求する、悪意のあるソフトウェアです。ユーザは一般的に、電子メールのフィッシング キャンペーンやエクスプロイト キットを通じてランサムウェアの被害を受けます。TeslaCrypt はランサムウェアの亜種としてよく知られており、世界中で多くの被害者が出ています。Talos の分析システムでも、よく検出されるランサムウェアの上位 5 位に入っています。TeslaCrypt 3 の中核的機能は、これまでと同様に、ユーザのファイルを暗号化してユーザに金銭を要求するメッセージが表示されるものです。
情報セキュリティ コミュニティは、配布メカニズムを妨害し、優れた検出方法を開発することでランサムウェアの脅威に対応してきました。しかし攻撃者も新たな技術の導入と進化を続けています。しかし不幸にも、この競争が TelsaCrypt の以前のリリースの再利用や改良を生み出す結果に繋がり、現在では TelsaCrypt 3 がリリースされています。ユーザを侵害するこの TeslaCrypt の最新亜種への対応に当たり、Talos は機能と仕組み、前回のリリースからの変更内容をより理解するために TeslaCrypt 3 のリバース エンジニアリングを行いました。
前の亜種には暗号化キーを保存する方法に弱点があったため、TeslaCrypt によって暗号化されたファイルを復号するツールを作成することができました [1]。しかし残念ながら、TeslaCrypt の今回の亜種については、まだそのようなツールは見られません。
この分析では、この記事の執筆時点で最新の TeslaCrypt 3.0.1 で使用されている暗号化アルゴリズムの概要を示します。わかりやすくするために、これ以降は TeslaCrypt 3 という名称を使用します。また、暗号化の詳細を、高校レベルの数学で理解できるように説明します。しかしいずれにしても、それなりに複雑な分析にはなると思われます。
楕円曲線暗号（ECC）に関する知識が十分でない場合は、先に進む前に「暗号化の基礎知識」（付録 B）を参照してください。またレポートでは、「暗号化の基礎知識」にある専門用語を使用します。
TeslaCrypt 3 のシンプルな暗号化スキーム
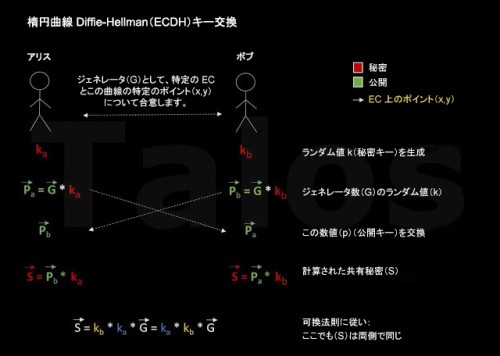
TeslaCrypt 3 の実際の暗号化アルゴリズムの細かい部分に入る前に、まずはシンプルな方法でアプローチしてみましょう。TeslaCrypt の関係者は、付録 B で説明されている ECDH アルゴリズムの微分を利用しています。
図 A
- 攻撃者はまず、公開キー（Pb）を作成し、ランサムウェア バイナリ ファイルに仕込みます。その後、そのランサムウェア バイナリ ファイルが PC（アリス）に感染します。
- これで、感染した PC（以後、アリスと呼びます）のランサムウェアは、ランダム値（ka）を計算できるようになります。
- これは、共有秘密（S = Pb * ka）に必要なすべての要素をアリスが持っていることを意味します。
- アリスは、一時的に生成された AES キーを使用してすべてのファイルを暗号化します。
- アリスは、ステップ 3 の共有秘密（S）の x 座標によって、この一時 AES キーを暗号化します。暗号化されたこの AES キーを「復元キー」と呼びます。
- ここからがポイントです。暗号化が完了すると、アリスの秘密キー（ka）と共有秘密（S）が削除されます。これは、アリスが式 S = Pb * ka を使用して共有秘密（S）を計算できず、復元キーを復号できないことを意味します。
- ただし共有秘密は、ボブ側の式 S = Pa * kb を使用して復元することができます。しかしアリスはボブ（C&C サーバ）の秘密キー（kb）を持っていません。これを持っているのは C&C サーバだけです。つまり C&C サーバだけが計算を実行できることになります。アリス（攻撃対象）は金銭を支払い、公開キー（Pa）を C&C サーバに送信します。これで、計算された共有秘密がアリスに返送され、復元キーの復号が可能になります。
実際には、TeslaCrypt 3 ではさらに複雑な実装が行われています。以下を参照してください。
実際の暗号化スキームと技術的な詳細
ここからは、TeslaCrypt 3 暗号化アルゴリズムの詳細に入っていきます。先に述べたように、この新しいバージョンは、弱い復元キー実装をクラックする [4] ための TeslaCrack[1] で使用されている因数分解攻撃を克服しています。因数分解攻撃は、総当たりで特定するよりも早く式の 2 つの因数を特定できるアルゴリズムです。前の TeslaCrypt の亜種では、2 つの因数は共有秘密と秘密キーであり、式「Recovery Key = Shared Secret Key * Private Key」が成立していました。
実装の不具合や選択された因数により、この因数分解には数秒で終わるものも、数日を要するものもありました。
新しいバージョンの TeslaCrypt では復元キーを生成する新しい方法を導入することで、この問題が修正されています。新しいバージョンでは ECDH アルゴリズムと AES 暗号化のある種のカスケード バージョンを使用して秘密キーが暗号化されています。さらに、対称暗号化キーとして、共有秘密の SHA256 ハッシュが使用されています。
例：Recovery Key = public key | AES256(private key, SHA256(shared secret))
つまり、因数分解に使用していたクリア テキストのキーが復元キーの中に残っていないことになります。詳細については以下を参照してください。
TeslaCrypt の実行と暗号化/復号のフロー：
開始時点では、いくつかのサンドボックス対策を実行した後で、ドロッパーはレジストリ値の「HKCU\Software\<derived from the workstation ID>\data」を開くことを試みます。後に、主要な設定をここに保存します。
中核的な暗号化機能は、主に GenerateMasterKeys、GenerateRecoveryKeys、GenerateAESRecoveryKey の 3 つの関数によって実行されます。前のバージョンで使用されていた関数は 2 つだけでした。
次のフロー概略図（図 B および図 C）とその説明で、暗号化と復号のプロセスを確認することができます。
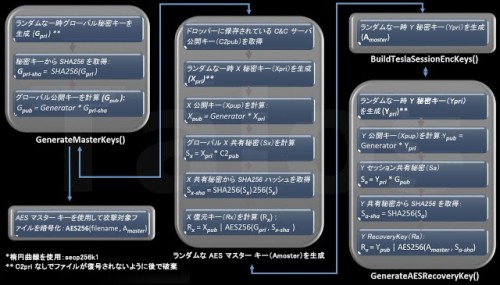
図 B – 暗号化プロセス
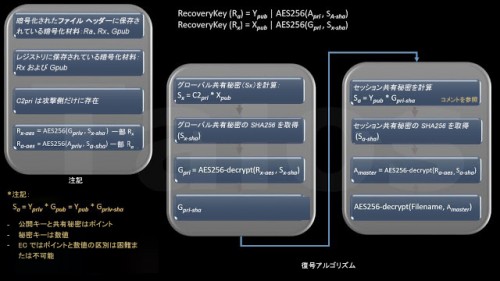
図 C – 復号プロセス
1.CheckKeyData：
前のバージョンの TeslaCrypt と同様に、このバージョンでもグローバル キーが生成され、さらに新しいセッション（暗号化プロセスの実行中にコンピュータが再起動された場合など）のたびにセッション暗号化キーが生成されます。グローバル キーは、グローバル復元キー（Rx）の作成に使用されます。セッション キーは、セッション復元キー（Ra）の作成に使用されます。これらはいずれもセッション共有秘密（Sa）の復元に使用されます。セッション共有秘密は、実際の AES マスター キーの暗号化に使用されます。AES マスター キーは、言い換えると、AES256 によってファイルを暗号化するために使用されるキーです。ドロッパーは最初に、グローバル キーの材料がすでに生成されているか、セッション キーの生成に直接ジャンプできるかを確認します。
図 D
2.GenerateMasterKeys
すでに述べたように、この関数は設定データ（グローバル キーの材料）がない場合、またはデータが無効である場合に呼び出されます。この関数によってグローバル マスター キーが生成されます。これらのキーは 1 回だけ生成されます。また暗号化プロセスが再開された場合にも再利用されます。このバージョンの TeslaCrypt で使用される新しいアルゴリズムでは、グローバル秘密キー（Gpri）が生成され、SHA256 が計算されます。この SHA256 からグローバル公開キー（Gpub）が導き出され、レジストリ データ値（offset + 0xB0）に保存されます。TeslaCrypt の作成者は、secp256k1 で標準化された楕円曲線を使用するため、Gpup = Generator * Gpri-sha 式内のジェネレータの値はそこで定義されます。
最終的に、Gpri を渡すことで GenerateRecoveryKey 関数が呼び出されます。このアルゴリズムは、最終的な復元キーの計算を除き、前のバージョンで使用されていたものと同じです。
3.GenerateRecoveryKey
このアルゴリズムは、C&C サーバの公開キーをドロッパーからインポートすることで開始します。TeslaCrypt では、公開キーの X および Y 座標がドロッパー内に保存されています。それらは「EC_POINT_set_affine_coordinates」ルーチンを使用してインポートされています。この時点で重要なステップが実行されます。まずランダムな一時秘密キー（Xpriv）が作成され、対応する公開キー（Xpub）が計算されます。「CalculateSharedSha256Secret」ルーチンでは C&C 公開キーと一時秘密キー（Xpri）に基づき、このレポートの最初のセクションで示した共有秘密の標準式を使用して、グローバル共有秘密キー（Sx）が計算されます。共有秘密の SHA256 が計算されて返され、GenerateRecoveryKey ルーチンに実行が返されます。この時点で、AES-256 CBC アルゴリズムによって、共有秘密の SHA256 を AES 暗号化のキーとして使用して、攻撃対象のグローバル秘密キー（パラメータとして渡される Gpri）が暗号化されます。一時公開キー（Xpub）と AES で暗号化されたグローバル秘密キー（Rx-aes）が最終的に連結され、次の方法で呼び出し関数に返されます。
+ 0x00 – Temporary EC public key (Xpub)
+ 0x41 – AES encrypted private key (Rx-aes)
GenerateMasterKeys ルーチンのアルゴリズムは、前のバージョンと同様に、「データ」レジストリ値の先頭の 0x30 バイトと「データ」レジストリ値末尾の起動時刻の加算をエンコードする、SHA256 および MD5 の計算で終了します。BuildTeslaSessionEncKeys 関数の実行に進みます。
4.BuildTeslaSessionEncKeys
この関数は、以前の TeslaCrypt バージョンの BuildTeslaEncKeys ルーチンに相当するものです。AES マスター暗号化キー（Amaster）は、CryptGenRandom API 関数を使用してランダム値を取得して、攻撃対象のワークステーションにある他のランダム データ（受信パケット数、プロセス数など）で拡張することで生成されます。最後に GenerateAESRecoveryKey 関数を呼び出し、ファイル暗号化セッションに属する復元キー（Ra）が計算されます。当然ながら、復元キー（Ra）は、暗号化プロセスが中断して再開されるたびに計算されます。
5.GenerateAESRecoveryKey
このアルゴリズムは、GenerateRecoveryKey 関数のアルゴリズムと似ています。ここでも一時公開キーと秘密キーのペアが生成されますが、C&C サーバの公開キー（C2pub）ではなくグローバル公開キー（Gpub）を使用して、共有秘密が計算されます。関数名に AES とありますが、これは依然として楕円曲線公開キー暗号化です。この名前がついているのは、最後に AES マスター キーの暗号化に使用されるためです。
GenerateRecoveryKey 関数と同様に共有秘密の SHA256 ハッシュが計算されますが、次に AES によって、グローバル SHA の共有秘密ではなく、SHA の共有秘密（Sa-sha）セッションを使用して、AES マスター キーが暗号化されます。返される復元キーは次のように構成されています。
+ 0x00 – Temporary public key (Ypub)
+ 0x41 – AES encrypted AES master key (Ra-aes)
BuildTeslaEncKeys 関数が正常に返されると、暗号化された各ファイルのオフセット 0 で記述されたヘッダーを含むバッファが生成されます。
次に、2 つの主要な場所に保存されたデータのサマリーを示します。
レジストリに問題が発生した場合に備えて、復号プロセスの重要データのバックアップを保存して、冗長性を確保してください。
設定のレジストリ データ：
| オフセット | 値 |
| + 0x30 | 16 進数（0x80 バイト）のグローバル復元キー（Rx） |
| + 0xB0 | SHA256 から生成されるグローバル公開キー（Gpub） |
| + 0xF8 | 起動時刻の QWORD |
暗号化されたファイル ヘッダー：
| オフセット | 値 |
| + 0x00 | 8 バイトの 0、8 バイトのランダム データ、8 バイトの 0 |
| + 0x18 | 16 進数（0x80 バイト）のグローバル復元キー（Rx） |
| + 0x98 | グローバル秘密キー（0x41 バイト）の SHA256 から生成されたグローバル公開キー（Gpub） |
| + 0xDC | 16 進数（0x80 バイト）の AES 復元キー（Ra） |
| + 0x15C | AES 初期化ベクトル（16 バイト） |
| + 0x16C | 元のファイル サイズ（4 バイト） |
TeslaCrypt の復号プロセス
ファイルのコンテンツの暗号化に使用された AES マスター暗号化キー（Amaster）を正常に復元するために、TeslaCrypt では設定レジストリ値およびファイル ヘッダーに保存されている復元キー（Rx）から処理を開始します。
1. 最初に次の式を使用して、対応するファイルのグローバル共有秘密（Sx）が次の式で計算されます。
global shared secret(Sx) = C&C private key(C2pri) * X public key(Xpup)
C2pri は、攻撃者だけが保有している秘密キーです。これは攻撃対象のマシンに送信または保存されることはありません。通常この式は、攻撃対象のマシンではなく C&C サーバで計算されます。このバージョンの TeslaCrypt の攻撃対象マシンにあるすべての暗号化ファイルは、この秘密キーで復号できます。これが攻撃者の大きな目標になります。グローバル X 公開キー（Xpub）は、グローバル復元キー（Rx）に保存されます。グローバル復元キーはレジストリに、またファイル ヘッダーにバックアップとして保存されています。
2. 次のステップでは、グローバル共有秘密の SHA256 を計算し、ユーザのグローバル秘密キー（Gpri）を復号します。
3. グローバル秘密キー（Gpri-sha）の SHA256 を計算し、AES 共有秘密（Sa）を再計算します。最初のセクションの EC の基本にある Sa = Ypri * Gpub = Ypub * Gpri-sha を確認してください。
4.SHA の AES 共有秘密（Sa-sha）を使用して、暗号化関数 AES256（Amaster、Sa-sha）の結果を逆算し、AES マスター キー（Amaster）を復号します。これは AES 復元キー（Ra）の第 2 部（Ra = Ypub | AES256(Amaster, Sa-sha)）に保存されます。
Amaster = AES256decrypt(Ra-AES, Sa-sha)
5. 最後にファイル復号プロセスを開始します。
Org. file = AES256decrypt(Encrypted-File, Amaster)
6. これで完了です。次のファイルに移ります。
まとめ
ここまでで、TeslaCrypt 3 が現在見られるランサムウェア システムの中で最高度の機能を持っていることを確認しました。強力な暗号化が可能で、攻撃者が使いやすい仕様になっています。C&C サーバで必要な計算はとてもシンプルです。それにもかかわらず、秘密キーは C&C サーバを離れる必要がなく、ランサムウェアは攻撃対象ごとに異なるキーを使用します。つまり、1 つの攻撃対象が金銭を支払ってファイル復号キーを取得しても、それはそのマシンでしか有効ではありません。
ここで強調すべきことは、ランサムウェアがインターネット上の大きな問題になっており、高度なエクスプロイト キットと無数のスパム キャンペーンによって拡散されていることです。攻撃者は変更と改良を続け、バージョンを更新しています。誰もが、AV ソフトウェアに検出されない新しいバージョンの攻撃対象になる可能性があります。復号ツールに依存せず、必ずバックアップを取り、最新に維持することが重要です。
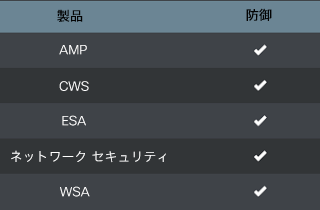
防御
Advanced Malware Protection（AMP）は、これらの攻撃者により使用されるマルウェアの実行の阻止に最適です。CWS または WSA Web スキャンによって、悪意のある Web サイトへのアクセスが防止され、これらの攻撃で使用されるマルウェアが検出されます。IPS と NGFW によるネットワーク セキュリティ防御では、最新のシグニチャによって攻撃者の悪意のあるネットワーク アクティビティが検出されます。ESA は、攻撃活動の一環として攻撃者が送信した悪意のある電子メールをブロックできます。
IOC
SHA256：
2FEA8FC0C2BD437D1BEAA49B0138E14619626F82D2A3F26209846C39D37DB6B0
8FC45DA2B164034DC558EC4E78A003EC8845A130AC2D305A5F33885C133E8062
362C4ACFCF96F5CD923C8C225D1EB968175C57854029154EECD9832E62B1ECF1
（バージョン 4 については現在調査中）
58318AED25FB94E053D3D0E2662D5358CEE6E444C2A1893E47DEA1E305E50581
カバレッジ
SNORT シグニチャ：
33893、34280、35788、35789、35790、35791、35792、35793、35794、37052
参考資料
[1] https://github.com/Googulator/TeslaCrack [英語]
[2] http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/ [英語]
[3] https://ja.wikipedia.org/wiki/楕円曲線
[4] http://www.bleepingcomputer.com/news/security/teslacrypt-decrypted-flaw-in-teslacrypt-allows-victims-to-recover-their-files/ [英語]
付録 B
暗号化の基礎知識：
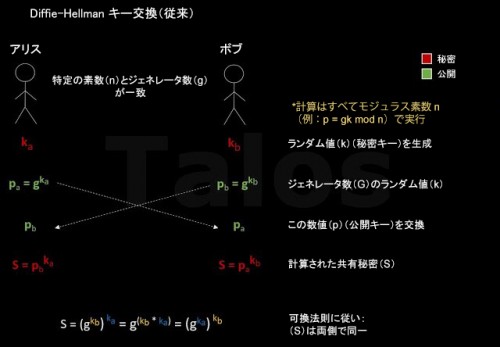
Diffie-Hellman：
次の図に示す Diffie-Hellman キー交換はよく知られています（図 E）。
図 E
簡単に言うと、ジェネレータ（g）は、たとえば 3 のような自然数で（グループ Z（p;*）のメンバーである必要があります）、モジュラス（n）は 7 などの素数である必要があります。セキュアな現実の実装では、（g）を小さい整数、（n）を非常に大きい素数（2048 など）にします（RFC3526）。数値の例：
ジェネレータ：（g）= 3
秘密キー：
アリスの秘密キー（ka）= 2
ボブの秘密キー（kb）= 5
公開キー：
pa = g^ka = 3^2 = 9 = 2（mod 7）
pb = g^kb = 3^5 = 243 = 5（mod 7）
共有秘密：
S = pb^ka = 5^2 = 25 = 4（mod 7）# 同じ共有秘密
S = pa^kb = 2^5 = 32 = 4（mod 7）# 両方で同じ
ネゴシエートされた共有秘密（S）は、AES などの対称暗号化機能で暗号化秘密キーとして使用できます。現実の実装では、共有秘密（S）は、通常、SHA などのハッシュ アルゴリズムによってハッシュされ、対称暗号化キーの長さとの互換性が確保されます。
楕円曲線暗号化（ECC）：
免責事項：以下の説明は ECC について網羅したものではなく、概略を示したものにすぎません。詳細については、ECC に関するインターネット上のドキュメントを参照してください。例：[2]
暗号化を理解するためには、ECC の前に Diffie-Hellman（DH）を説明するのがよいでしょう。離散対数は扱いづらく、a^x = b mod n は PC で簡単に計算できても、x = dLog_a * b は計算が複雑で時間がかかるためです。しかし特定の状況下では、従来の DH アルゴリズムは、ECC のアルゴリズムに比べて暗号化攻撃（指数微積分など）に対して脆弱になります。もう 1 つの利点として、短いキーで同じまたは高い強度の暗号化を実現できることです。バイナリにキーを埋め込むマルウェアに必要なメモリが少なくなります。
出典：http://www.nsa.gov/ia/programs/suiteb_cryptography/
楕円曲線（EC）自体は暗号化アルゴリズムではありませんが、離散対数に基づくアルゴリズムと組み合わせることで暗号化アルゴリズムになります。楕円曲線 Diffie-Hellman（ECDH）や楕円曲線 DSA（ECDSA）などがそれに当たります。これを楕円曲線暗号（ECC）と呼びます。詳細については後で説明しますが、まず楕円曲線とは何かを確認しておきましょう。
楕円曲線にはさまざまな種類があります。それらを暗号化アルゴリズムで使用するには特定の基準を満たす必要がありますが、それについてはここでは説明しません。EC の 2 つの例を以下に示します（赤い線）。暗号化について重要な点は、これらの曲線上のポイントを加算または乗算できることです（例：P1 + P2 = P3）。
グラフ上で、ポイント間（P1 と P2 など）に線を引き、曲線と再度交差するポイントを第 3 のポイントとして追加できます（このルールの例外についてはここでは取り上げません）。このポイントから y 軸と平行に線を引き、その線が曲線と交差する点が加算の和になります。結果は当然ながら、曲線上のポイント（P3）になります。次を参照してくだ
さい。
図 F
ポイントの乗算もほぼ同じ方法で行うことができます。ポイント自体にポイントを追加する場合（P1 + P1）、すなわち P1 * 2 の乗算を行う場合は、P1 から P2 に引いた線ではなく、ポイント（P1）の接線を使用することになります。
図 G
これを繰り返して、P1+P1+P1（P1 * 3 または P1+P1+P1+P1 = P1 * 4 と同じ）などを計算できます。
同じことを式を使用してコンピュータで実行することもできます。2 つのポイント P1 と P2 があり、これを加算して P3 を求めるとします。P1 と P2 が異なるポイントである場合と、P1 と P2 が同じポイントである場合を次に示します。P の上の矢印は、座標系の x 座標と y 座標から導き出されたポイントであることを示します。
図 H – Weierstrass の詳細については [3] を参照
楕円曲線では既知の演算（加算、乗算、累乗）を行えることがわかりました。
最も重要なことは、ECC ではポイントと数の乗算（P2 = P1 * 3 など）を簡単に実行できても、反対の演算である除算（P2/3 など）は簡単ではないということです。総当たりによって結果を導くしかありません。
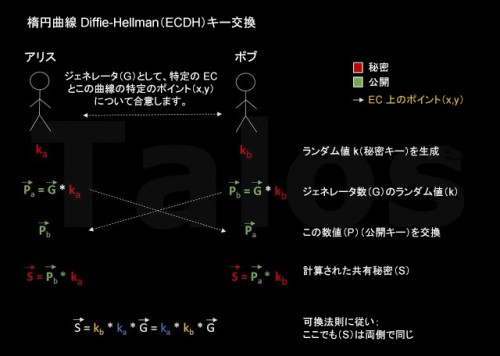
言い換えれば、上記から DH アルゴリズムでは EC を使用することができ、EC 上のポイントでジェネレータ（g）を置き換えることができるということです。この例ではこれを G で示します。楕円曲線については、secp256k1 などの標準があります。この標準によって、G となる曲線上のポイントが定義されます。ポイントの乗算ができるため、G がポイントであって従来の DH のような数ではない場合でも、式 P = G * kb（以下を参照）は完全に機能します。G がある数字によって乗算されると、結果はまた曲線上のポイント（P）になります。以下の図に、完全な ECDH アルゴリズムを示します。前に示した図と似ていますが、ここでは数字ではなく EC 上のポイントを使用します。
図 I
重要な点は、openssl などの現実の実装では、1 つの座標だけ（通常は x 座標）が共有秘密（S）から導き出され、さらに計算が行われます。この x 座標は大きな数値であり、ポイントではありません。
DH で EC ポイントをジェネレータとして使用すると、離散対数問題は、攻撃者にとってさらに解決が困難になります。アルゴリズムでは、いわゆる暗号のスムーズさが高いほどよいことになります。それによって、暗号化アルゴリズムにランダム値を与えて、結果の数字が大きいか小さいかを推測する、総当たりによる暗号化データの復号を効率化することが、不可能または非常に困難になります。たとえば 2^3 = 8 という計算で、式の 8 と 2 だけが既知で、3 を求めるとします。まず 5 などのランダム値を使用して 2^5 = 32 を計算します。32 が 8 より大きいことから、次は 5 より小さい値を試す必要があることがわかります。そのため従来の DH では、対数係数を計算していました。上記の例で係数 9 を使用するシステムでは、結果は 2^5 mod 9 = 5 になります。この場合、次の試行で大きい値と小さい値のどちらを使用すべきかを推測するのが困難になります。実システムの離散対数問題は、係数がこの例の 9 よりも大幅に大きく、暗号のスムーズさが補完されます。ECC システムではこれらのポイントのランダム性が大幅に高くなるため、値が小さいか大きいかを推測することが非常に困難または不可能になります。
本稿は 2016年3月16日に Talos Group
Authors